“Intricacies of Feature Geometry in Large Language Models” by 7vik, Lucius Bushnaq, Nandi
LessWrong (30+ Karma)
Shownotes Transcript
Audio note: this article contains 157 uses of latex notation, so the narration may be difficult to follow. There's a link to the original text in the episode description.
Note: This is a more fleshed-out version of this post and includes theoretical arguments justifying the empirical findings. If you've read that one, feel free to skip to the proofs. We challenge the thesis of the ICML 2024 Mechanistic Interpretability Workshop 1st prize winning paper: The Geometry of Categorical and Hierarchical Concepts in LLMs and the ICML 2024 paper The Linear Representation Hypothesis and the Geometry of LLMs. The main takeaway is that the orthogonality and polytopes they observe in categorical and hierarchical concepts occurs practically everywhere, even at places they should not.
** Overview of the Feature Geometry Papers** Studying the geometry of a language model's embedding space is an important and challenging task because of the various [...]
Outline:
(01:00) Overview of the Feature Geometry Papers
(06:22) Ablations
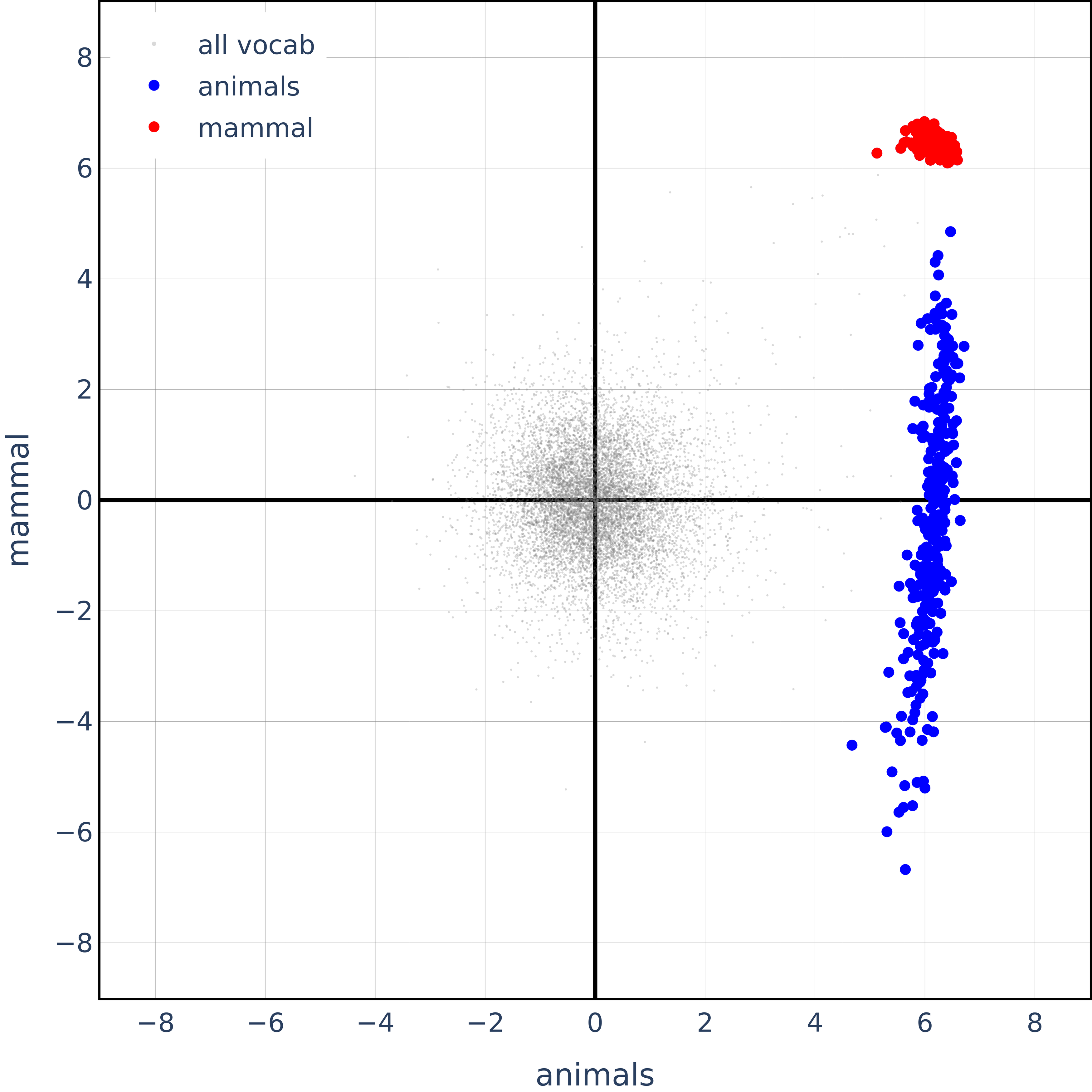
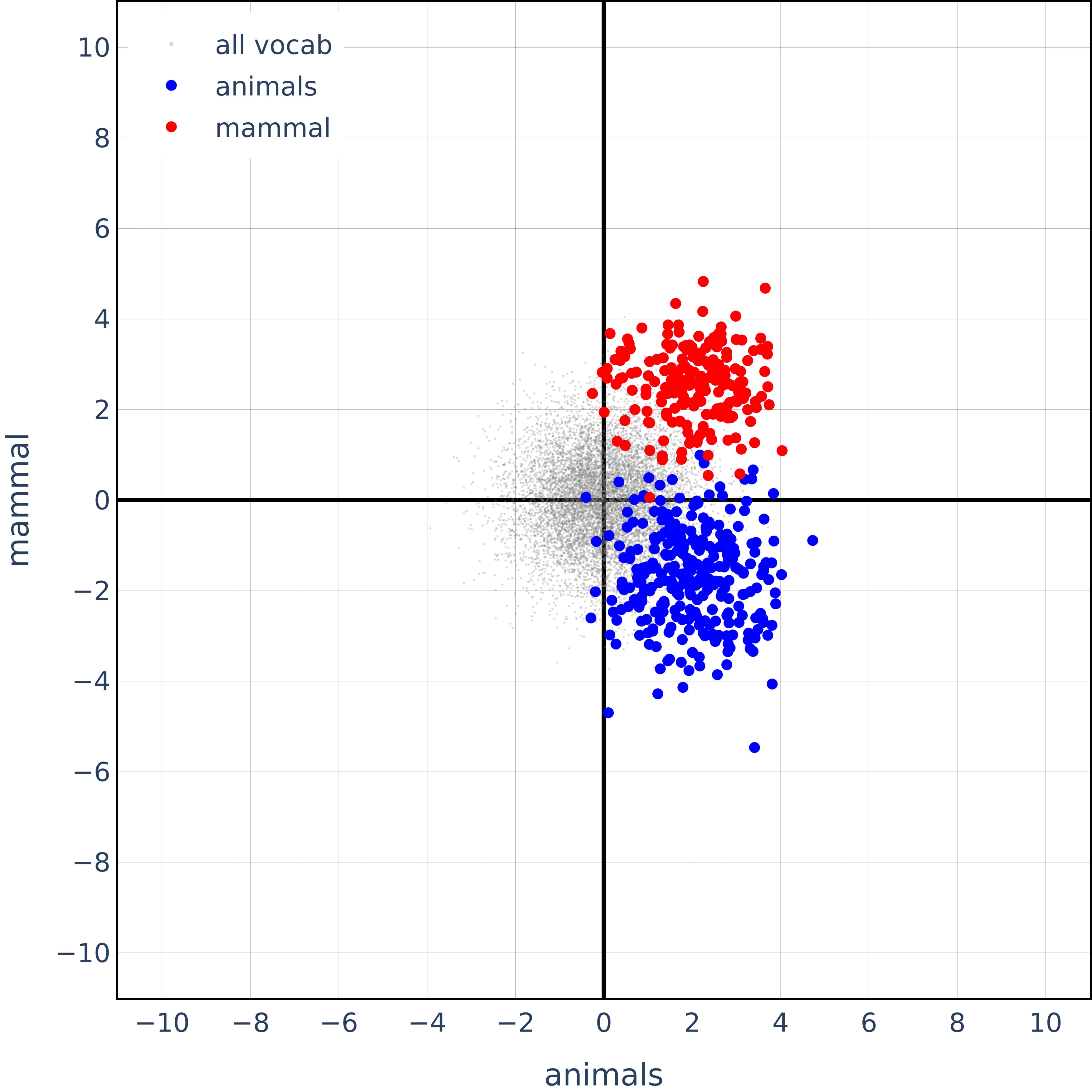
(06:32) Semantically Correlated Concepts
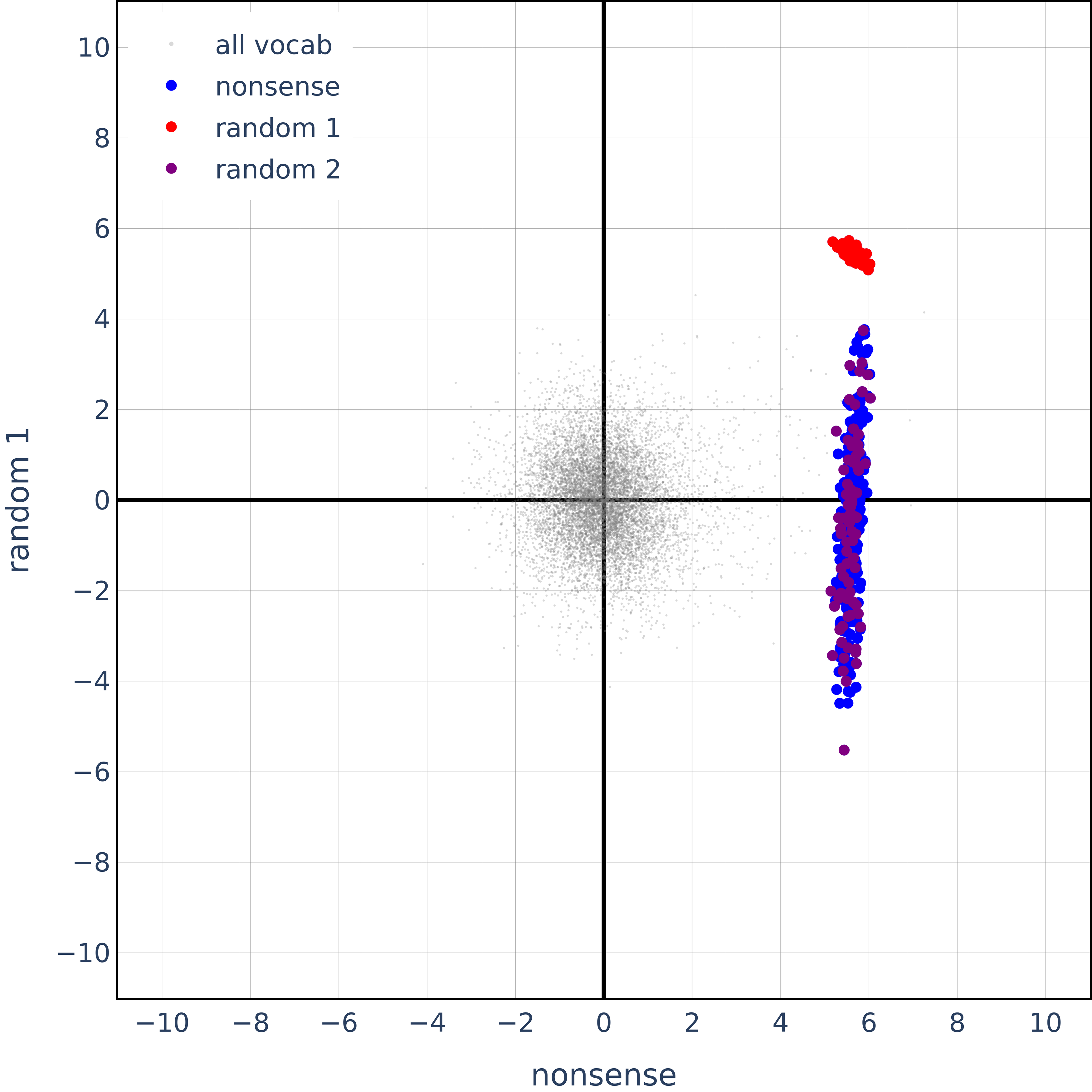
(06:57) Random Nonsensical Concepts
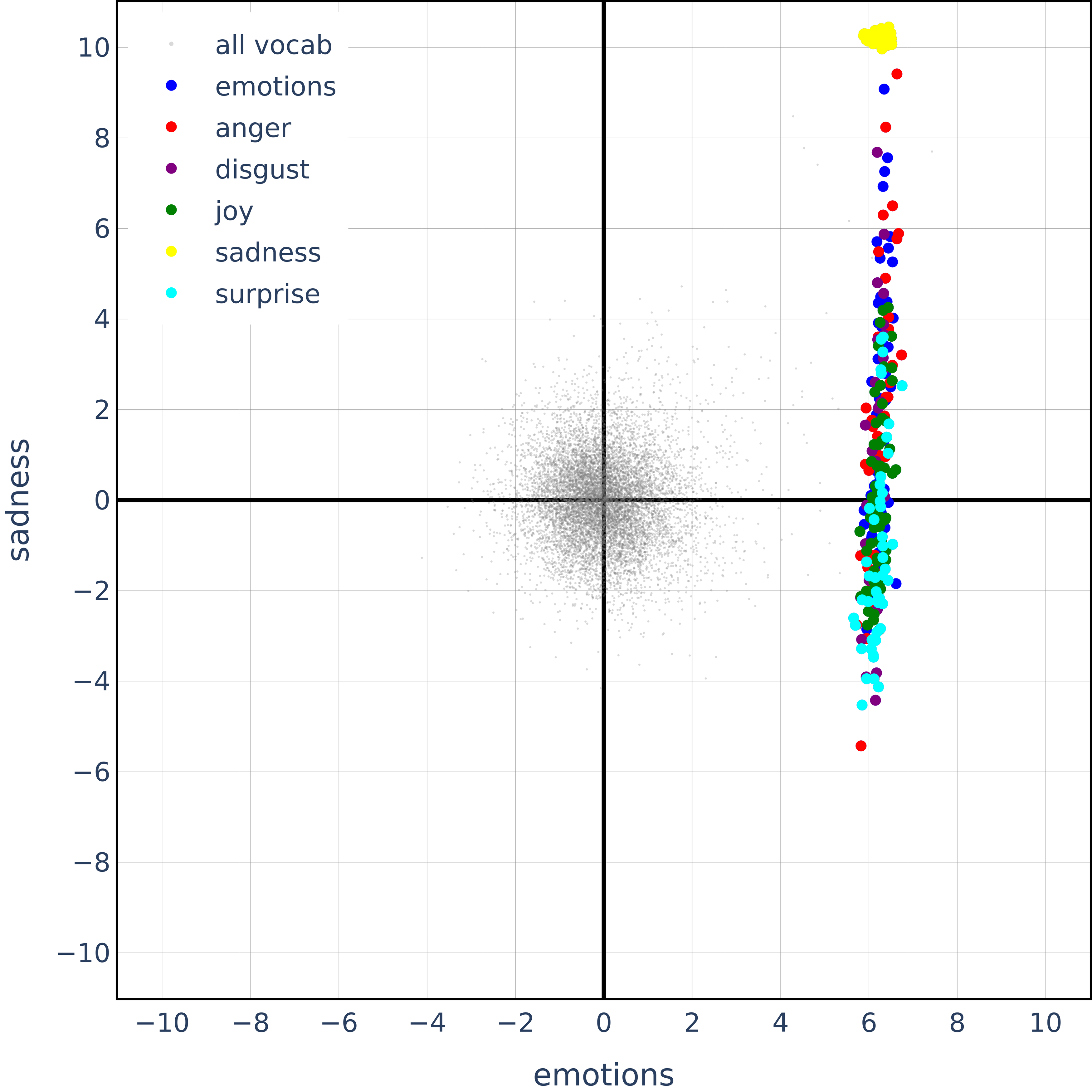
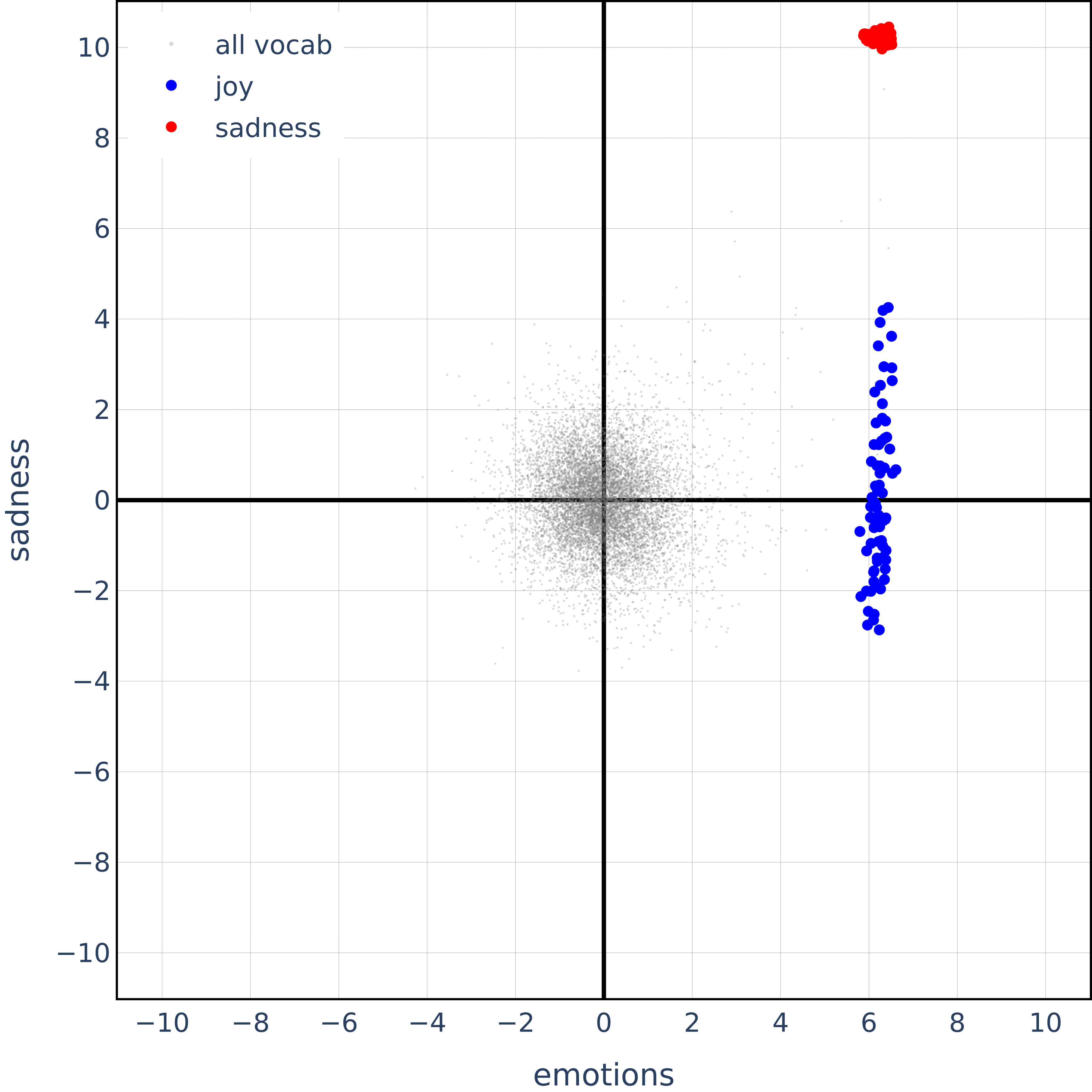
(07:32) Hierarchical features are orthogonal - but so are semantic opposites!?
(09:15) Categorical features form simplices - but so do totally random ones!?
(09:54) Random Unembeddings Exhibiting the same Geometry
(10:55) Orthogonality and Polytopes in High Dimensions
(11:23) Orthogonality and the Whitening Transformation
(13:12) Case n\geq k:
(17:21) Case _n
(19:59) 2. High-Dimensional Convex Hulls are easy to Escape!
(21:32) Discussion
(21:35) Conclusion
(22:07) Wider Context / Related Works
(23:38) Future Work
The original text contained 6 images which were described by AI.
First published: December 7th, 2024
---
Narrated by TYPE III AUDIO).
Images from the article:
)
)
)
)
)
)
)
Apple Podcasts and Spotify do not show images in the episode description. Try Pocket Casts), or another podcast app.