134 烦恼的时候，我就想想正弦函数
20:47 Share

大家好,我是门童,欢迎收听严肃喧哗最近马上过年了嘛我听到很多朋友已经回到家乡然后分享了很多跟家人发生的烦恼所以我就想跟大家分享一下通常来说我应对烦恼以及应对无聊的方法乍一听可能有点离谱是做数学题

但这里面其实是很有门道的今天呢我就先给大家分享一下我对于正弦函数的爱如果有不喜欢数学的朋友也希望听到这里不要先插掉因为我们今天要聊的内容一定不会很枯燥我自己之前其实有很多当家教的经历

那如果我是给一个幼儿园小朋友解释正弦函数的话呢我可能会带他去海洋馆看海豚的表演我会说小姑娘你看海豚在水里跳跃它每完成一次跳跃呢它都会达到一个最高点然后回到水里后也会落到一个最低点所以正弦函数呢它就是记录着这样海豚跳跃的高度变化当然了他也有可能听不懂

那我也会带它再去荡秋千我说你看我总会把你推到一个最高点然后你会快乐的荡回到最低处那然后呢又飞向天空再飞荡回来这种有节奏的上下荡一样的起落就是振显函数

而如果我是给一个小学生解释正弦函数的话我会带他去看海我会说你看那里的潮汐还有波浪它们起伏摆动着永不停息我也会给他带纸和笔而且是最全最多的那种 108 色的油画棒就是我小时候很羡慕的那种因为我家人基本上就给我买 24 色所以我会教小朋友把它观察到的海浪画下来

那无论是日出的金光闪闪还是暮色的隐月清灰当他勾勒出波浪起伏的曲线的时候我就会告诉他无论是潮汐潮落或者是秋冬春夏当我们想用数学来表达这种重复的话就可以使用 sin x 而终于等他上了中学的时候他已经知道了直角三角形知道了圆知道了角那我就会教他定义三角函数的不同办法

那最简单的呢,我们是以直角三角形来定义直角三角形就是有一个直角和两个锐角我们随便命名其中一个锐角的度数为θ而 sinθ的值就等于对边比斜边当然这位同学可能会问为什么这个角要叫θ这是因为无论是奠定几何传统的数学家欧吉里德还有阿基米德

还是创造了使用圆的弦长来计算角度这个概念的天文学家西帕克斯他们都是古希腊人而θ就是他们所使用的一个希腊字母长得就像一个 0 中间又画了一口所以今天在学校在高等数学里面大家见到角度往往就会想到用θ来表示这是一种从公元前就约定俗成的惯例而我们中国人也是沿袭的这种习惯而已

如果你不想用θ你可以用任何希腊字母比如说α,β,γ如果你不想用希腊字母你也可以用任何名词来指代你可以说 sin 公保基丁那这个公保基丁是 30 度的锐角或者 cos 砸猪排那这个砸猪排呢是 90 度的直角都可以当然砸猪排如果是 90 度的

那这是定义正弦函数的方法之一

请注意我们使用的动词是定义是发现而不是发明不是创造因为无论有没有人类这个函数都会存在这些规律比人类更早就存在于这个宇宙然后咱们再聊另外一种正弦函数的定义方法首先请大家想象一个平面值叫做标系然后有一个点叫做 P

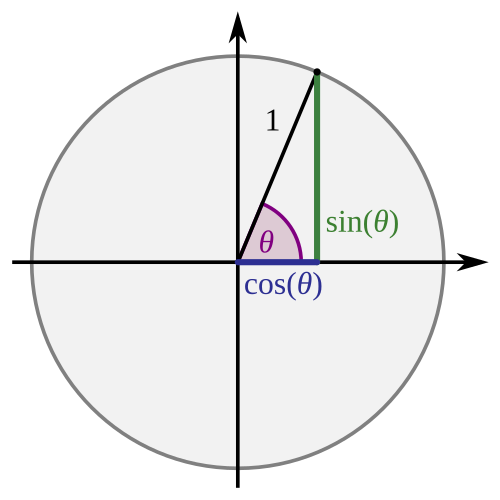
P 的横坐标是 X,纵坐标是 Y 我们把这个 P 点跟圆点连一条线再把 P 点垂直往 X 轴上画一条线就可以构成一个直角三角形而在这个直角三角形里刚才我们把 P 和圆点连成的线就跟 X 轴交叉形成了一个角

我们还是把这个角叫做θ假设 p 点跟原点的距离是 1 那根据我们刚才那个正弦函数的定义 sinθ就等于对边比斜边而斜边是 1 的话而我们刚才也说了 p 点的坐标是 xy 对边就是这个点的高度也就是 y 所以 sinθ就等于 y 除以 1 等于 y 而把这个等式颠倒过来看那就是 y 等于 sinθ那同理呢 x 就等于 cosθ

possion 是余弦嘛那一个角的余弦就等于另外一个护余角的正弦也就是说余弦函数呢它可以看作是正弦函数向左或者向右平移了 90 度后得到的一个函数所以它们的波形在形状上一致的指示风和谷的位置存在一个相位差而

换句话说在一个半径为一的单位圆里就譬如我们刚才说到的那个点 PP 到原点的距离就是 1 所以 P 它可以看作是单位圆上的一个点所以从代数的视角来看我们要再引入一个毕达格拉斯横等式而这个横等式就是一个直角三角形

两条直角边的长度的平方和等于斜边的平方那毕达哥拉斯老师也是希腊人由于他们古代把较短的直角边称为钩长而把较长的直角边称为骨长所以这个毕达哥拉斯横等师还有一个名字叫做钩骨定理

而当然正弦函数,余弦函数它们除了代数也有微分上的关系比如正弦的导数是余弦而余弦的导数是负正弦但我们今天先不聊导数所以我们说回正弦函数的第二个定义 P 的坐标是 xy 而 x 等于 cosθy 等于 sinθ这个定义方法就叫做单位元定义法而说到了元我们就要再说说ππ就是我们小数背的 3.1415926

那π是怎么被发现的呢我们先随意画一个标准的圆我不知道大家以前上美术课的时候有没有上过第一课就是美术老师会让大家画一个标准的圆不要去用圆规划然后用自己的笔画出来所以一整堂课大家都可能都在那里画圈圈而且那个时候电视台里好像刚好正在放西洋洋语回态了

里面就有一个人物叫做潇洒哥潇洒哥也喜欢画圈圈所以我们画出了这样一个圆如果用直尺来测量这个圆形的直径再用卷尺来测这个圆的周长我们就会发现周长除以直径也就是这两个数值的比值它们永远约等于一个数 3.14 而这个数呢就是人类发现的圆周率π

而π这个常数呢它适用于宇宙所有的元常数的意思就是固定不变的数值嘛像我们人生里面我们跟亲人的关系可能就是个常量但是像朋友恋人的关系可能就是变量如果我们希望把一个恋人变成我们的亲人那可能就要进行从变量到一个常量的转换

那有一个问题就来了正弦函数的那种波浪曲线是怎么画出来的呢当我们把刚才想象的坐标轴的 x 轴换成角度也就是θ大家想象一个横着的坐标轴它从 0 度开始然后往右边 10 度 30 度 60 度 90 度这就是一个横着的θ轴

而纵坐标就是这个角度所对应的 sin 函数的值也就是 y 等于 sinθ我们从 0 度开始把 sin0,sin1,sin2 对应的 y 轴上的数值这样的一个点标注出来我们就会发现对应着横轴跟纵轴的点它们就能连成一条曲线这个曲线就是正弦函数的曲线

而需要强调的一点是某些正弦函数的值它们并没有一个准确的值比方说我们肯定背过 sin 30°等于 0.5 而 sin 90°等于 1 但是 sin 45°的值就是√1 而√2 我们知道它是一个无理数

大家也做过那种题如何证明根号二是个无理数不过我们今天就不证明了我想说的是由于很多正弦函数的值它是一个无理数它像π一样无穷无尽所以很多人在计算的时候选择一个精度就会存在误差比方说当希腊文化传播到古印度的时候印度人就继续研究了三角数他们

公元五世纪末的时候有一个数学家叫阿耶波多他提出了用弧所对应的弦长的一半来对应半弧的正弦而后面的古印度的数学家也用了这种做法其实跟我们现代的正弦函数的第三种定义一致而更具体的定义方法我们今天就先不聊而

等到时间拉到了 15 世纪的时候阿拉伯的数学文化呢又传回了欧洲因为那会儿我们之前的专题节目聊过啊就是欧洲的商业就开始兴盛起来比方说两亚西班牙葡萄牙他们开始航行他们开始地理测绘的时候就出现了对于三角学的需求所以当他们在翻译阿拉伯的数学著作的时候欧洲的数学家呢就开始制作更详细精确的三角函数的指表什么是这个三角函数的指表

大家肯定也见过这张表格就是不同的度数它所对应的正弦函数的值当我们拿到了这样一张表在实际应用的过程中我们就不用算了我们可以直接用那张表比方说我们给一条斜坡施工那如果我们知道这个斜坡的角度和它垂直的最高高度的话

我们就能根据这个表的比例算出这个斜坡的大致长度这个斜坡其实就是我们直角三角形中的斜边而在各个场景的应用中都可能会存在这样一个直角三角形对应的斜边比方说对船的一些建造比方说一些地理的测绘比方说很多建筑领域的测绘像金字塔每个金字塔里面就有很多的三角形

古代的人民怎么保证它是一个对称的结构以及在搬运这个建筑所需要的材料的时候如何来估算它大致需要的材料数量还有它累积的角度呢这里面都会用到三角函数指表但是如果是在天文学里面的话再小的误差都可能会被放大到非常严重因为距离太远了比方说我们知道 sin30°等于 0.5°

那 sin31 度具体等于多少呢所以这个时候就需要泰勒级数的出现当然这个时候除非是上了很多课外班或者是竞赛班大概率当我们了解到这个概念的时候我们已经来到了大学那泰勒级数呢它就是用一大串的多项式去无限逼近某个函数就有点像我们假设有一个拼图 puzzle 的任务原本呢它是一幅难度极高的拼图比方说我之前拼过签名上合图

当我们把它拆成很多个小块也就是对应着多项式中的每一项我们每多拼一块就能多还原一点真实的画面当我们拆的无限小拼到无穷快的时候就会完美重现这个函数所以简单来说的话泰勒技术就是给你一个多项式的包让你用拼凑的方式去近似或者再现那些平常我们不容易去直接计算的函数

而泰勒展开就是把这个函数写成无穷级数的一个过程或者说把函数表达为泰勒级数的一个操作当然还有像是欧拉公司也会用到正线函数但是里面还有虚数我们今天就先不说总而言之从数学结构的本身来看只要存在圆只要存在直角三角形就必然会派生出正线函数以及相关的三角函数

更宽泛的讲只要有周期性的运动有旋转的运动都会用到阵线函数比方说最早对于阵线函数产生兴趣的就是天文学家这是因为他们发现了行星绕日或者是行星绕地这样的一个运动在天空中呈现了一定的周期性这种日月星辰的周期往复就激发了那些古代文明对于周期函数的思考

而如果要精确的刻画出这些周期函数那自然就需要跟圆周运动相适应的一些数学描述比方说在经典力学里面减斜正子就是比方说一个弹簧正子或者是一个小正弧的单摆就像我们上一期节目聊到的钟摆一样这些减斜正子所满足的微分方程的通解也是正弦函数跟余弦函数包括

包括无论是声波电磁波还有水波它背后都能分解成振显形式的波动模式这也就是说自然界中的很多振动波动现象也是以振显函数为核心原型的比如现在大家听到我的声音这是因为在手机或者音频设备的内部首先它已经把声音的信号给数字化了也就是转化成了很多个采样点而在数字域中我们都知道它是一串 010101

但本质上它依旧可以对应一条模拟的波形而且在播放的时候数字信号又会被一个数模转化器就是 DAC 变回成了一个模拟的电压或者是电流的波形而这个模拟电压信号它会驱动喇叭或者是我们使用的各种耳机里面的发声单元来振动音模进而音模的快速振动会挤压空气产生一个疏密相间的声波这些声波

它就可以在时间轴上拆分成很多不同频率的正弦波的叠加那当耳朵接收到了这些波就能还原成大家所听到的我的声音那如果大家使用的是蓝牙耳机的话蓝牙呢它就是靠电磁波在一个 2.4GHz 左右的频段传输这个数字的信息而电磁波呢它

它本身也在物理上可以分解为正弦波分量只不过频率很高而数字调制技术它就会把这些信号编码成某种频率或者是某种相位上对应的变化但归根结底这些变化都是基于一个载波的正弦振荡再叠加上一些调制的信息再比方说我们人类的呼吸我们在安静状态下我们的呼吸就是呈现出一个平稳的一呼一吸的循环

那如果拿一个简单的测量装置比方说一个胸部的呼吸带去监测我们胸廓或者是腹部的一个扩张还有收缩随着时间变化的曲线我们就会看到一个类似于阵线波波动的形状因为它也带有明显的周期性它有它波峰和波谷的一个缓慢的变动

所以总而言之无论是空气声波无论是耳机的振膜还是电磁波还是我们人体的生理信号只要有周期的振动它都可以用振线函数来描述或者做拆解振线函数它就是最简单的周期曲线也是所有线性波动中最基本的数学形态

而且就算我们所观察的一个现象一个场景里它不是一个完美的周期它也可以让我们在局部或者一定区间内做类似的频谱分析而如果思路再打开的话比方说百年孤独里面的马孔多这个小镇它在命运的潮起潮落一次次也在经历相似的变化

他们这一代又一代的人就像正弦波一样也遵循着这种循环往复的时间上的韵律再比方说托斯托耶夫斯基的《罪与法》主人公呢他其实也是在道德在信仰在他的灵魂间进行着这种起起落落的内心的波动我们也可以把这种起落视作是一种精神世界上的正弦

因为我们的感受我们的情绪它不可能说一直停留在某一个极度的兴奋也不会一直陷入在一个永久的绝望里它就是在这些正极和负极之间荡来荡去我们人生中面对很多事情的心态就会像郑贤波这样上下起伏

那再比如说康德的纯粹理性批判我们总是先得到经验来感受自然世界的循环然后再由理性来构建出一个抽象函数那感性跟理性这些鲜艳和经验之间的关系就是像这些函数一样也是周期性的迭代的那再比方说村上春树的海边的卡夫卡或者是 EQ 巴斯或者是刺杀七十团长那本书在村上的笔下也总是交织出现出

孤独的现实跟一个平行的梦境村上笔下的人物总是在这样一个现实跟梦境之间游走这也很像是一种周期性的往返我们每个人生命的脚本也可能出现这种相似但又不同的情节我们再看看那些历史上王朝的兴衰无论是中国古代的朝代的循环还是世界范围内我们讲很多帝国的兴起很多帝国的瓦解

他们都是更宏观意义上的正弦波从蓬勃发展到顶峰再缓缓的下滑然后又被新的力量所替代从文景之治到东汉末年从开元盛世又到安史之乱而我们具体的每一个人我们人的一生他从出生到死亡再到新生再到死亡是一样一个循环而人的每一天呢我们从吃饭然后再到拉把拔

这里面也有很多循环这些循环里有有机物跟无机物的转化它有微观的亮变和宏观的质变中间的变化那我们看月亮月亮有阴晴圆缺我们看伊斯兰教的很多建筑的图案里面也有很多正弦波的形态组合

我们弹钢琴的时候钢琴的每一个音的振动都近似正弦波而且和声学的原理也表示越是和谐的音程它正弦波的频率比就越简单再像是西方经济学中也早就注意到一些经济的周期复苏繁荣衰退萧条然后又复苏而且这些经济周期在不断的被验证

我们之前节目聊过的很多国家比方说美国的民主制度下政党的轮替也是有一定规律的在保守派他们执政数年后人们就又更倾向于自由派但一个自由派如果施政过久的话民意又会出现新的摇摆所以当我烦恼的时候或者

当我无聊的时候我就会想一想正弦函数当我们人类还没有出现的时候正弦函数它就已经存在于宇宙即使我们看不见它但它不以任何人的意志为转移的这样存在着不同的人类民族可能有不同的信仰不同的习惯或者是不同的争执但是比方说一个德国人跟一个以色列人他们不可能同时发现两个不一样的正弦函数

正弦函数它是唯一的无论人们怎么打打杀杀如何四处迁徙如何在喜怒哀乐悲欢离合里面挣扎痛苦纵欲欢笑正弦函数都在那安静的存在着无论人类是赶春运还是放圣诞假正弦函数它都是存在于这个地球乃至整个宇宙它承载着不计其数的自然规律还有社会隐喻

但无论是什么

但无论如何,正弦函数它都像我们最开始告诉幼儿园小朋友那样,正弦函数就是海浪,它永远起伏摆动,它永远不停歇。我们日常生活中不计其数的烦恼,在正弦函数那里只不过就是沧海一粟,能从欧吉里德、阿基米德到我们 21 世纪的人类,这只不过都是弹指一挥尖。

那以上就是我本期节目的所有分享非常感谢大家的收听有任何想法和建议都欢迎随时交流喜欢本期节目的话也欢迎帮忙转发推荐或者打赏祝大家假期有个好心情我是门童我们下期见